- Yes, my partner's claim is true. Firstly, we have to show that every
frequent itemset in the lattice is either itself complete or is a subset
of a complete-frequent itemset. That is, the set of complete-frequent
itemsets forms a ``cover'' for all frequent itemsets. This proof will
ensure that we know the identities of all frequent itemsets.
Proof: Let
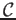 be the set of complete-frequent itemsets, for
each of which we are also provided the associated supports. Let
be the set of complete-frequent itemsets, for
each of which we are also provided the associated supports. Let 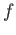 be a generic frequent itemset in the lattice. If
be a generic frequent itemset in the lattice. If
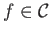 ,
then its support is known trivially. Otherwise, let
,
then its support is known trivially. Otherwise, let 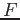 denote the
itemset obtained by the ``round-trip'' operator on
denote the
itemset obtained by the ``round-trip'' operator on 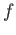 , that is,
, that is,
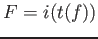 . Now,
. Now, 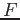 has to be a superset of
has to be a superset of 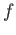 (because, if
(because, if 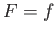 ,
,
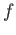 would be complete, and if
would be complete, and if
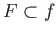 , the definition of round-trip
operator is violated). So, we can be sure that with every incomplete
, the definition of round-trip
operator is violated). So, we can be sure that with every incomplete 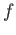 ,
there is an associated complete(superset)
,
there is an associated complete(superset) 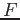 . Futher, the associated
. Futher, the associated 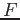 has
to also be frequent, since its support is exactly equal to that of
has
to also be frequent, since its support is exactly equal to that of 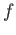 ,
again by the definition of the round-trip operator. Therefore, it will
be in
,
again by the definition of the round-trip operator. Therefore, it will
be in 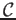 . Finally, by the subset-frequency property enumerated
in the Apriori paper, every subset of a complete-frequent itemset will
also be frequent.
. Finally, by the subset-frequency property enumerated
in the Apriori paper, every subset of a complete-frequent itemset will
also be frequent.
So, the above shows that
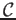 is a ``cover'' for
is a ``cover'' for 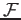 ,
the set of all frequent itemsets.
,
the set of all frequent itemsets.
- Yes, we can derive the supports of all frequent itemsets from
the associated cover, using the following algorithm:
Do a bottom-up lexicographic traversal of the complete-frequent-itemset lattice - that is, first consider all 1-item complete-frequent itemsets, then all 2-item complete-frequent itemsets, etc. Maintain a dynamic set
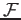 and for each complete itemset
and for each complete itemset 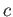 encountered in the
traversal, enumerate all subsets of
encountered in the
traversal, enumerate all subsets of 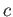 and enter those subsets not
already in
and enter those subsets not
already in 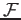 into
into 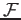 , along with the associated
, along with the associated 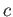 .
.
At the end of the above traversal, we will have a list of all frequent itemsets along with their associated complete-frequent itemsets. Now the support of each frequent itemset in
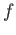 in
in 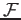 is simply
computed as the support of its associated
is simply
computed as the support of its associated 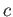 .
.
NO, Variance is an algebraic aggregate function.
The variance of a random variable X is defined as
![]() . This can be re-written as
. This can be re-written as
![]() .
.
![]() and
and ![]() denote
denote ![]() which is an algebraic function,
since it can be computed from a 2-tuple consisting of
which is an algebraic function,
since it can be computed from a 2-tuple consisting of ![]() and
and
![]() . Based on the above formula, a 3-tuple
. Based on the above formula, a 3-tuple
![]() is sufficient to compute the variance. Thus
a fixed size result can summarize the sub-aggregation implying that the
Variance is algebraic.
is sufficient to compute the variance. Thus
a fixed size result can summarize the sub-aggregation implying that the
Variance is algebraic.
An easy way to decide the choices is to realize that there is really
no point in picking up views ![]() and
and ![]() since their size is exactly
the same as
since their size is exactly
the same as ![]() . So, if we add up the space used by materializing
all the remaining views, that comes to less than 7.12M, which is within
the bound of 12.5M. Now, neither
. So, if we add up the space used by materializing
all the remaining views, that comes to less than 7.12M, which is within
the bound of 12.5M. Now, neither ![]() or
or ![]() can be (pointlessly)
added after this since including them would exceed the 12.5M bound.
So, the final choices for materialization are
can be (pointlessly)
added after this since including them would exceed the 12.5M bound.
So, the final choices for materialization are
![]() .
.
The monotonicity property is that the benefit of any non-selected
view monotonically decreases with the selection of other views. That
is,
![]() ,
where
,
where ![]() is the original lattice and
is the original lattice and ![]() are the selected views.
The monotonicity property is important for the greedy heuristics to
deliver competitive solutions. If the optimal solution can be partitioned
into disjoint subsets such that the benefit function satisfies the
monotonicity property with respect to each of these partitions, then the
greedy heuristic guides, at each stage, the selection of an optimal set
of views within these partitions.
are the selected views.
The monotonicity property is important for the greedy heuristics to
deliver competitive solutions. If the optimal solution can be partitioned
into disjoint subsets such that the benefit function satisfies the
monotonicity property with respect to each of these partitions, then the
greedy heuristic guides, at each stage, the selection of an optimal set
of views within these partitions.
A rectangle
![]() contains another rectangle
contains another rectangle
![]() if the following conditions hold:
if the following conditions hold:
![]() and
and
![]() . This is similar to the structural join in the Timber paper, where we check if the begin and end of an xml element are contained within the begin and end of another xml element.
. This is similar to the structural join in the Timber paper, where we check if the begin and end of an xml element are contained within the begin and end of another xml element.
An upper bound can be obtained by building a joint position histogram on all 4 attributes
![]() . Let
. Let ![]() be the histogram from table
be the histogram from table ![]() and
and ![]() for table
for table ![]() and assume that we have
and assume that we have ![]() buckets along each dimension. For any tuple in the bucket
buckets along each dimension. For any tuple in the bucket ![]() of
of ![]() , the number of tuples it joins with in
, the number of tuples it joins with in ![]() is given by
is given by
![]() . Thus the upper bound is given by
. Thus the upper bound is given by
![]() .
.
Using the left-to-right sequence is important in order to maintain the clusters in sorted order which then requires only a ``merge-join'' of the join relation clusters.
- The reason for settling with radix-based hashing (which is not a particulary good randomizing function) in the paper is that the computation of high-quality randomizing hash functions will itself involve (a) excessive load on the CPU and, more importantly, (b) cause cache misses due to the invocation of the hashing function and its data values.
L1 cache miss cost ![]() = 5 cycles and L2 cache miss cost
= 5 cycles and L2 cache miss cost ![]() = 55 cycles.
= 55 cycles.
- Consider node size to be the L1 cache line size. Thus
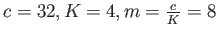 . Each node access leads to one L1 miss and one L2 miss. Number of nodes accessed,
. Each node access leads to one L1 miss and one L2 miss. Number of nodes accessed,
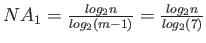 . The total cost is thus
. The total cost is thus
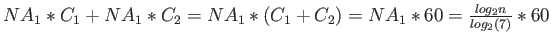 cycles.
cycles.
Consider node size to be the L2 cache line size. Thus
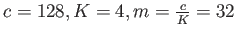 . Each node access leads to four L1 misses (since L1 cache line size is
. Each node access leads to four L1 misses (since L1 cache line size is
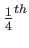 of 128) and one L2 miss. Number of nodes accessed,
of 128) and one L2 miss. Number of nodes accessed,
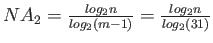 . The total cost is thus
. The total cost is thus
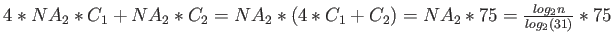 cycles.
cycles.
It can be seen that it is better to have a node size of 128 bytes.
- If node size is 32 bytes, number of L1 and L2 cache lines accessed is
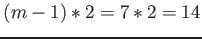 . Thus the total cost is
. Thus the total cost is
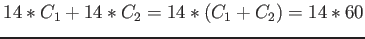 cycles.
cycles.
If node size is 128 bytes, number of L1 cache lines accessed is
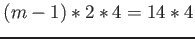 and the number of L2 cache lines accessed is
and the number of L2 cache lines accessed is
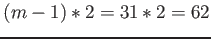 . Thus the total cost is
. Thus the total cost is
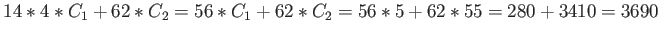 cycles.
cycles.
It can be seen that the split cost is lower if the node size is 32 bytes.
Yes, I agree with the claim. The join algorithm is as follows:
